a bit of obfuscation: MBA expressions, opaque predicates, affine functions

0x00 - start point:

in this article, we will cover "what is MBA Expressions" as the main topic. but while we are talking about this subject, we will also talk about techniques such as Opaque Predicates for a full understanding of everything. It might be a long post. so if you're determined to read, you'd better make your coffee before you start.

0x01 - introduction:

MBA Expressions, which stands for Mixed Boolean Arithmetic, is one of the most common principles used by many obfuscators.  MBA Expressions are used to confuse the data flow of the program using boolean operators, (e.g., ∧,∨,¬,⊕) and integer arithmetic  operators, (e.g + (ADD) , * (IMUL) , -  (DEC) ) operators.

As shown in the picture above, a simple addition process in the first picture can be converted to a more complex and difficult MBA expression using arithmetic and bitwise operators. In other words, the main purpose of MBA expressions is to reduce the clarity of simple process patterns by turning them into more bloated and complex patterns.

We can make a simple introduction by rewriting the x+y equation, one of the most common MBA expressions.

x + y == (x ^ y) + 2 * (x & y)

here we rewrite the equation x+y, which is basically the sum of two unknown values, using arithmetic and boolean operators (x ^ y) + 2 * (x & y). and for every value you give to these two functions, the result of both functions will be equal. In other words, to explain in the basic obfuscation logic, these two equations are equal to each other. the only difference is that one is in its simplest form and the other is a bit more complicated using MBA expression.

0x02 - a little math:

in this part, we will use some math knowledge. then let's mix the above function a bit more. we have 1 function and 1 inverse function. these functions are affine functions. Unlike normal functions, affine functions rely on overflow.

Note: MBA expressions often use affine functions. basically the formula is f(e) = (a * e) + b. usually a,b are n-bit constants and e is our MBA subexpression. 

our first expression: E₁ = (x+y) and our f(x) and f -1(x) functions (affine function):

(f: x -> 39x + 23    /  f -1: x -> 151x + 111)

let's apply the rule (E2) we rewritten in the previous screenshot to E1;

E₂ = (x ⊕ y) + 2 × (x ∧ y)

1. in step 1, we wrote the E2 subexpression where we saw x in our f(x) function.
2. in the 2nd and 3rd steps, we wrote the E2 expression where we saw x in the f -1(x) function, the same as the function we did above, and we got the E3 expression.
3. we expand the E3 expression we obtained in step 4 and we come across an example obfuscated MBA expression.
   

mathematically these 3 functions are equal to each other and therefore they will give the same result. our basic principle here is to make the expressions more complex with bitwise and simple arithmetic operators.

0x03: a bit of "affine functions"

and if you've probably read another article before, you must have seen the same equation 39x + 23. Let's try to explain a bit where this equation comes from. (as much as my math knowledge)

f(x) = ax + b (mod 2ⁿ)

in order to use this function, we need a one more affine function ( g(x) = cx + d ). but these f and g functions we find must be inverses of each other. ie f(g(x)) function must be equal for each value of x.

so to summarize simply;

f(x) = ax + b (mod 2ⁿ)

g(x) = cx + d (mod 2ⁿ)

f(g(x)) == x // for every x value

in simple math principles, if you write f(x) where you see x in an f -1 (inverse) function it should equal the same result as the function itself.  f-1 (f(x))  = f(x) 

to be sure of the existence of such a function, the coefficient a of f(x) must be prime between 2ⁿ. Considering this point, since we are using mod 2ⁿ, a must be an odd number for this function to be suitable for mod 2ⁿ.

here is the mathematical point where the 8-bit (2⁸) affine function (f: x -> 39x + 23 / f -1: x -> 151x + 111), which is used in all articles and we have also used :=)

before I get into MBA simplification, I would like to talk about a few more common techniques used with obfuscation. because most techniques are not usually used alone. A stronger structure can be obtained by blending many techniques with each other.

0x04 - Opaque Predicates:

as the name suggests, the opaque predicates technique is the technique of inflating the control flow by placing meaningless code blocks that will never work between the code blocks that the program will process during normal operation.

an example of a normal branching chart should look like this picture. the branches are significant and short. but when opaque predicate is used the control graph becomes horrible like this;

i hear your cursing. if we look a little closer, we will understand everything completely;

an example is an opaque predicate block. In this block, arithmetic operations are applied to two variables and at the end of the block, the equality of these two variables is checked. but since these two variables will never be equal, the code always branches in the same direction. Let's explain a little more clearly with images

in my next blog post, I will note that I am not good with anything about design.

it creates a code block that will never be interpreted by subjecting x and y variables to arithmetic operations such as multiplication, addition and subtraction step by step. this has no effect on code execution, because the code never branches to a different point. the purpose here is to make it harder for the reverse engineer to make sense of the control graph.

we will need an SAT/SMT solver to confirm the correctness of this equation.

finally, let's show why this code block will not be interpreted with a simple python code and continue with MBA simplification.

Using the z3-solver module in python, we checked the equation model we obtained from the assembly code to see if this equation has any binary solution. and the program returned "unSAT" (unSATisfiable). If you get the answer unsat, it means that there is no model that solves the equation.

if there was any solution model, he would return the answer to sell to us. let's make our equation solvable and see the positive output.

since we removed the subtraction of - 1, when 0 is given instead of x in both equations, the result will be equal to 0, so the two equations have a common solution model and the program returned the sat response from the check() function. By using the model() function, we have printed the model that provides us with these two equations.

(we made a small introduction to opaque predicate simplification. I will explain it in more detail in another article. for now, that's enough to know.)

0x05: MBA Simplification:

droidguard lib-*.so library graph view

MBA expressions are frequently used in many popular applications, ransomware, application libraries today. The image I have attached above belongs to the lib-*.so library of the DroidGuard VM running in the core of Android. We can see a heavy use of MBA in the various functions in this library (the graph was getting longer, but I didn't reduce the image further for clarity :=] ).

in this article, we will use the mba_challenge file shared by Tim Blazytko. 

we can see lots of XOR, AND and ADD instructions :=) let's prepare a python script using the miasm module and see the MBA expression of the block here.

output:

{((((((((RSI[0:32] ^ 0xFFFFFFFF) & RDX[0:32]) + RSI[0:32]) ^ 0xFFFFFFFF) & RDX[0:32]) + ((RSI[0:32] ^ 0xFFFFFFFF) & RDX[0:32]) + RSI[0:32]) & (RDX[0:32] ^ 0xFFFFFFFF)) + -(((((((RSI[0:32] ^ 0xFFFFFFFF) & RDX[0:32]) + RSI[0:32]) ^ 0xFFFFFFFF) & RDX[0:32]) + ((RSI[0:32] ^ 0xFFFFFFFF) & RDX[0:32]) + RSI[0:32]) | (((RSI[0:32] ^ 0xFFFFFFFF) & RDX[0:32]) + RSI[0:32])) + ({RDI[0:32] & ({RDI[0:32] & RSI[0:32] 0 32, 0x0 32 64} * 0x2 + {RDI[0:32] ^ RSI[0:32] 0 32, 0x0 32 64})[0:32] 0 32, 0x0 32 64} * 0x2 + {((((RSI[0:32] ^ 0xFFFFFFFF) & RDX[0:32]) + RSI[0:32]) & RSI[0:32]) + (((RDI + {(RDI[0:32] ^ 0xFFFFFFFF) | RDX[0:32] 0 32, 0x0 32 64} + 0x1)[0:32] ^ 0xFFFFFFFF) & RDX[0:32]) + (RDI[0:32] ^ ({RDI[0:32] & RSI[0:32] 0 32, 0x0 32 64} * 0x2 + {RDI[0:32] ^ RSI[0:32] 0 32, 0x0 32 64})[0:32]) + ((RDI[0:32] ^ 0xFFFFFFFF) | RDX[0:32]) + (RDI + RDX + 0x1)[0:32] 0 32, 0x0 32 64})[0:32]) * 0x2 0 32, 0x0 32 64}

calm down, we'll get over this soon. i will briefly talk about the code block so that the article does not go any further.

we generated a symbol table variable (loc_db) from the LocationDB class. we opened the mba_challenge file in a Container. then we derived a Machine() class and created a compatible type Machine by giving its architecture the architecture of our example file (mba_challenge).

after these definitions, we init a disassemble engine with the dis_engine function and set the start address of the disassemble function with dis_block.

then we create a new IR (Intermediate representation) variable using our lifter object that we created using our symbolic table variable. and with the help of add_asmblock_to_ircfg() function to this IR object, we give our IR variable (ira_cfg) and our variable containing the value of the code we disassembled at the target address. (asm_block)

then we derive an object from the SymbolicExecutionEngine class and with the help of this object, we execute a symbolically execute from the start address we have defined. 

finally, since we want to obtain the expression, we return the data carried by the RAX register by giving the arch type of our lifter variable.


well, now that we've explained the code, let's simplify this expression a bit.

output:

{(((RDI[0:32] + RSI[0:32]) << 0x1) + RDX[0:32]) * 0x2 0 32, 0x0 32 64}

it's a little less scary now :=) 

here we have implemented a simplification using the Simplifier class of the Msynth code deobfuscation framework. we've found the little expression where the huge long expression we've just seen is actually equal :=)

basically, the MBA technique works on the same principle on the code as we explained above with mathematical functions. Just as we make a simple x+y equation very complex with mathematical methods, when we apply similar principles on the code side, we come across mixed MBA expressions.

there are many tools available (Qsynth, Msynth etc..) to simplify MBA expressions, but I used msynth in this article as it was the most satisfying to me in terms of performance and results.

All materials used in the article can be found at https://github.com/Ahmeth4n/ahmeth4n.github.io/tree/master/mba address. i hope it was a useful article :=). see you later.

thanks for:
Tim Blayztko - https://www.youtube.com/watch?v=_TsV0RXoIQE

Arnau Gamez - https://github.com/arnaugamez/talks/tree/main/2022/01_r0-workshop

how does safetynet work? (fight with instagram)

hello from new year! (i'm starting to write the article on 31.12.2022. i'm wondering too when i can finish and publish it :=D) i dont like for new year nights but okay, no problem. today, i will explain safetynet structure and safetynet attestion api reverse engineering on this post.

What is the "SafetyNet"

basically SafetyNet is an API developed by google that implements various procedures to ensure code security in Android application. google Play services must be installed on your device in order to use the Safetynet APIs. 

SafetyNet verifies your application by performing tests called CTS (Compatibility Test Suite) on your application. basically it checks criteria including device root status, OEM lock status, google play version, security of device traffic (sniffing or not?), app signature, etc.

SafetyNet performs an attestation (SafetyNetApi.attest()) operation using these safety parameters. As a result of the attestation process, a JWT response will be returned to you according to the information reported from your device.

in this JWT token we have 2 boolean values with keys ctsProfileMatch and basicIntegirty. These values are the values that show whether your device is marked as safe in line with the examination of SafetyNet safety parameters.

apart from these values, it also contains values such as your package name (apkPackageName), sha256 signature of your apk file (apkDigestSha256), sha256 hash of your apk certificate (apkCertificateDigestSha256).

CTS Profile Match: bootloader unlocked?, custom ROM?, uncertified device? etc..
Basic Integrity: is an emulator?, rooted device?, any agent injected? (frida etc..) etc..

if you fail the Basic Integrity and CTS Profile Match tests, your application will likely flag you. speaking for Instagram, it blocks your account until a certain date as soon as you create an account. each app may react differently.

SafetyNet WorkFlow

well, i hope  we understood the part of "what is a safety net and basically how does security work?". our next step SafetyNet WorkFlow.

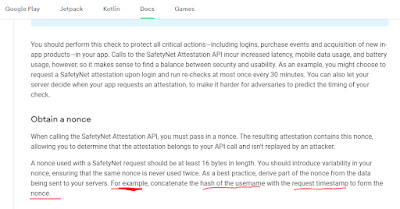pic 1.1

(keep in mind the underlined text in this picture. we will come back this picture later)

1 - to use safetynet, you must create an API key for yourself from the Google API Console and include this API key in the application. safetynet receives a nonce value from you and an API_KEY value to validate your API. (this "nonce" value must be unique.) If the values you provide are correct, you will receive a JWT token response. If the information you provide is incorrect / suspicious, an error message will be returned to you.

attestation api basically works with a "nonce" value. the length of this value is 16 bytes. as stated in the android developer document, you can convert this value into a hash as you wish. but it will be a 16 byte value that safetynet needs. 

this value generate from mobile app side. request is sent to the safetynet API from the mobile application with this created "nonce" value.

2 - safetynet works integrated with DroidGuard. SafetyNet result and droidguard result are considered together in data reported to GMS side. this data you create is sent to GMS Core. GMS Core creates a protobuf message using this data. (proto schematics: https://github.com/microg/GmsCore/blob/ad12bd5de4970a6607a18e37707fab9f444593a7/play-services-core-proto/src/main/proto/snet.proto#L15-L25)

basically, this message contains information such as your gms version, package name of your application, signature hash. and here it reports whether your device is rooted in the suCandidates parameter and the SELinux status in the seLinuxState parameter.

now let's reinforce a little on instagram. let's make a little fridascript and list the gms classes.

Java.perform(function() {
    Java.enumerateLoadedClasses({
        onMatch: function(className) {
            if(className.includes("android.gms")){
				console.log("founded classes: " + className);
			}
        },
        onComplete: function() {}
    });
});

output:

we examined the classes of the com.google.android.gms package, which is the standard package name of GMS, with a simple fridascript. Before proceeding to the review, a class in the class names should have caught your attention :=)

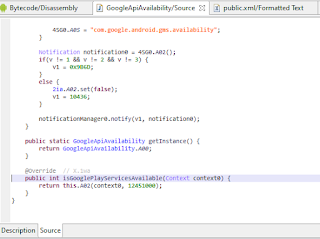
if you noticed, let's take a closer look at the 'com.google.android.gms.common.GoogleApiAvailability' class

let's review A02 class

the most basic step of the safetynet, "google play services installed? can it be available?" The class where the control is done on Instagram. this class checks google play services on your device and sends an error message when sending safetynet report if google play services is not available or unavailable on your device.

this method basically check google play services existing status, signature validations and google play services update status (outdated or updated). this is one of the simplest principles of GMS that we mentioned above. let's make sure it's called by hooking the function call with frida

Java.perform(function() {
    var google_api = Java.use('com.google.android.gms.common.GoogleApiAvailability');

    var google_api_hook = google_api.isGooglePlayServicesAvailable.overload("android.content.Context");
    google_api_hook.implementation = function(context0) {
        console.log('\n hooked: '+ context0);
		var return_val = google_api_hook.call(this, context0);
		console.log("return value: " + return_val)
        return google_api_hook.call(this, context0);
    };
});

response:

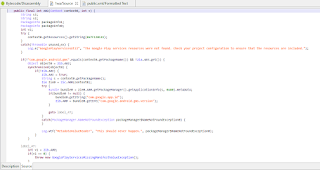
yep, called :=) isGooglePlayServicesAvailable function arguments are context value for current context and int value for google play version. The int value checks if google play services is outdated. context value is current context data.

int variable "v" check line

as an example, I simply tried to show you the point where it detects the google play service. but applications also have various controls other than that. therefore, you may need to analyze not only the GMS side, but also the entire application and intervene in the control points. since we focus on SafetyNet in this article, I do not elaborate on these issues.

now that we've shown an example, let's dig a little deeper!

SafetyNet Attestation Analyze on Instagram

let's start with capturing traffic. you can capture traffic with this fridascript on github, it works. i intercept all the requests up to the account creation step and reviewed the post data in the account creation step.

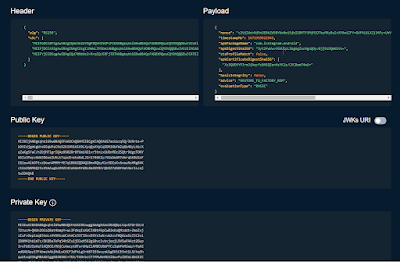
well, we encountered the sn_nonce value :=)  base64 is a value and when we decode it as you can see in the picture, we see a structure like this. 

yes the email address in base64 is not the same as in the picture. because I used temp-mail to sign up.

does this remind you of anything? yep, same on pic 1.1 :=) 

when generating the Instagram safety nonce value, it uses your email address + current timestamp + and random 24 byte parameters that you used during registration. to separate them | uses the bracket.

another point that draws our attention is that the isGooglePlayServicesAvailable function of GMS, which we have just mentioned, is called here again :=) that is, they call the same function once again and provide control.

let's examine one by one.

stringBuilder0.append(s);

since the value of s comes as an argument to the function, it is directly appended to the payload. this value corresponds to the email address.

  long v = System.currentTimeMillis() / 1000L;
  

this line divides timestamp by /1000 to match its format in payload. Thus, it creates the 2nd parameter, the timestamp.

byte[] arr_b = new byte[24];
new SecureRandom().nextBytes(arr_b);

and generates a 24-byte random value using SecureRandom(), which is the last stage of the payload. and finally, after each process;

stringBuilder0.append("|");

 it completes the payload by adding its "|" separator. 

well, we got how to generate sn_nonce payload. after this step i prepared a small frida script by following the functions to see 2 different outputs on the emulator and on the real device. let's see the frida script and its output.

  /*

com.instagram.nux.deviceverification.impl.VerificationPluginImpl.startDeviceValidation(android.content.Context, java.lang.String) : void
Descriptor: Lcom/instagram/nux/deviceverification/impl/VerificationPluginImpl;->startDeviceValidation(Landroid/content/Context;Ljava/lang/String;)V

target package: package com.instagram.nux.deviceverification.impl;

*/

function googlePlayAvailable(){
	var GoogleApiAvailability = Java.use('com.google.android.gms.common.GoogleApiAvailability');

	var GoogleApiAvailability_isGooglePlayServicesAvailable_0 = GoogleApiAvailability.isGooglePlayServicesAvailable.overload("android.content.Context");
	GoogleApiAvailability_isGooglePlayServicesAvailable_0.implementation = function(context0) {
		console.log(`[+] Hooked com.google.android.gms.common.GoogleApiAvailability.isGooglePlayServicesAvailable(context0)`);
		var return_call = GoogleApiAvailability_isGooglePlayServicesAvailable_0.call(this, context0);
		console.log("isGooglePlayServicesAvailable() return value before changing: " + return_call);
		return 0;
	};
}

function xCaj(){
	var CAj = Java.use('X.CAj');

    var CAj_init_0 = CAj.$init.overload("java.lang.String", "java.lang.Integer", "java.lang.String");
    CAj_init_0.implementation = function(s, integer0, s1) {
		console.log("safetynet params - CAj$init got:")
        console.log(`[+] Hooked X.CAj.$init(s, integer0, s1)`);
		console.log(s);
		console.log(integer0);
		console.log(s1);
        return CAj_init_0.call(this, s, integer0, s1);
    };
}

function startDeviceValidation(){
	var VerificationPluginImpl = Java.use('com.instagram.nux.deviceverification.impl.VerificationPluginImpl');

    var VerificationPluginImpl_startDeviceValidation_0 = VerificationPluginImpl.startDeviceValidation.overload("android.content.Context", "java.lang.String");
    VerificationPluginImpl_startDeviceValidation_0.implementation = function(context0, s) {
		console.log("safetynet generate function - startDeviceValidation() got:")
		console.log(s);
		console.log(context0);
        console.log(`[+] Hooked com.instagram.nux.deviceverification.impl.VerificationPluginImpl.startDeviceValidation(context0, s)`);
        return VerificationPluginImpl_startDeviceValidation_0.call(this, context0, s);
    };
}

function safetyInner(){	
	var x5Vo = Java.use('X.5Vo');

    var x5Vo_A0w_0 = x5Vo.A0w.overload("java.lang.String", "java.lang.StringBuilder");
    x5Vo_A0w_0.implementation = function(s, stringBuilder0) {
		console.log("safetynet function inner - A0w() return:");
		console.log(s);
		console.log(stringBuilder0);
        console.log(`[+] Hooked X.5Vo.A0w(s, stringBuilder0)`);
        return x5Vo_A0w_0.call(this, s, stringBuilder0);
    };
}


function safety_probably(){
    var x9dr = Java.use('X.9dr');
    var x9dr_init_0 = x9dr.$init.overload("X.4eo", "java.lang.String", "[B");
    x9dr_init_0.implementation = function(x4eo0, s, arr_b) {
        console.log(`[+] Hooked X.9dr.$init(4eo0, s, arr_b)`);
		console.log("class val:")
		console.log(x4eo0);
		console.log("string val: " + s);
		console.log("byte val:")
		console.log(arr_b);
        return x9dr_init_0.call(this, x4eo0, s, arr_b);
    };
}

function feedback_required(){
    var x2So = Java.use('X.2So');
    var x2So_A03_0 = x2So.A03.overload("X.3m7", "X.1Id");
    x2So_A03_0.implementation = function(x3m70, x1Id0) {
		console.log("x3m70" + x3m70);
		console.log("x1Id0" + x1Id0);
        console.log(`[+] Hooked X.2So.A03(3m70, 1Id0)`);
        return x2So_A03_0.call(this, x3m70, x1Id0);
    };
	
}

Java.perform(function() {
    xCaj();
	startDeviceValidation();
	googlePlayAvailable();
	safetyInner();
	safety_probably();
	feedback_required();
});

  

response from emulator:

meh, we got error. because google services not installed on emulator. so it returned an error that it could not find the gms core safetynet api.

i changed the return value of the isGooglePlayServicesAvailable function to 0 in fridascript. because 1 fail is defined as 0 successful value.

let's see the output of the same script on real device

great! we got jwt. but if we decrypt this jwt, we will see that everything is not ok :=)

we mentioned basicIntegrity and ctsProfileMatch values above. you see it's "false" here :=) because the device is rooted, OEM unlocked and there are too many detectable components inside.

SafetyNet has different error messages for each situation. For example, if we had re-signed this apk, we would have received another signature-related error this time. but now it returns basicIntegrity and ctsProfileMatch values as false because it realizes that the device's ROM has changed. If you take a look at the advice value, you will see "RESTORE_TO_FACTORY_ROM", that is, restore the rom settings :=)

when you connect to your device from adb and type sestatus, you will understand why it gives this error :=)

in this article, if I explain how we can make these values true, that is, how we can pass the control mechanisms, the article will be too long. It's been long enough with its current state :=) so I'll leave the rest for the next post.

let's finish this article by basically dealing with the issue of safetynet and working in an application as an example. see you in another article!

you can also find the fridascripts used in the github repo at this link.

thanks for:

https://www.romainthomas.fr/publication/22-sstic-blackhat-droidguard-safetynet/

https://www.blackhat.com/docs/eu-17/materials/eu-17-Mulliner-Inside-Androids-SafetyNet-Attestation-wp.pdf